Zipf's Law and Why We Turn Words Into Numbers

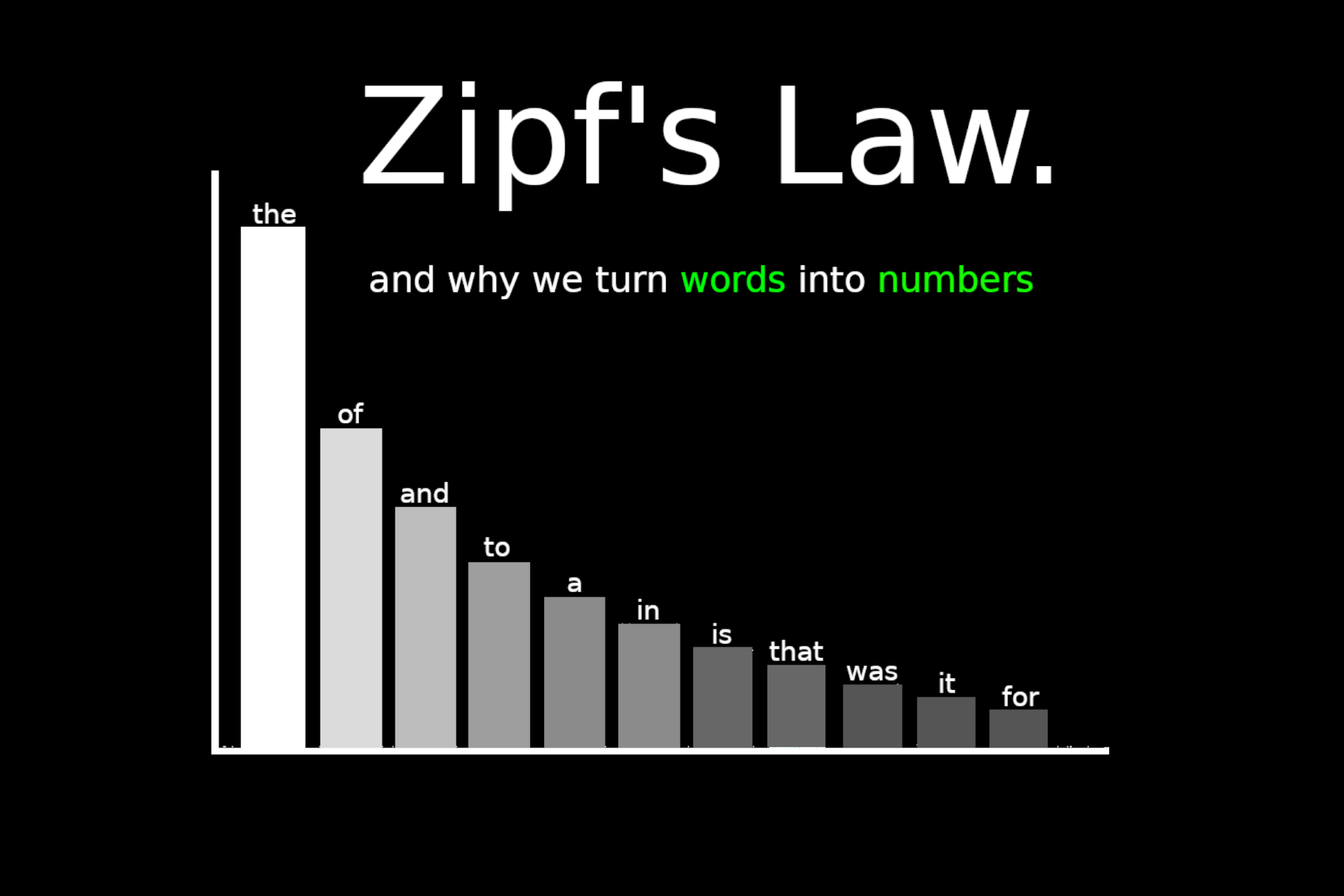
Here's something weird about language: if you grab any book, article, or even your text messages and count how often words appear, you'll find the same pattern every single time.

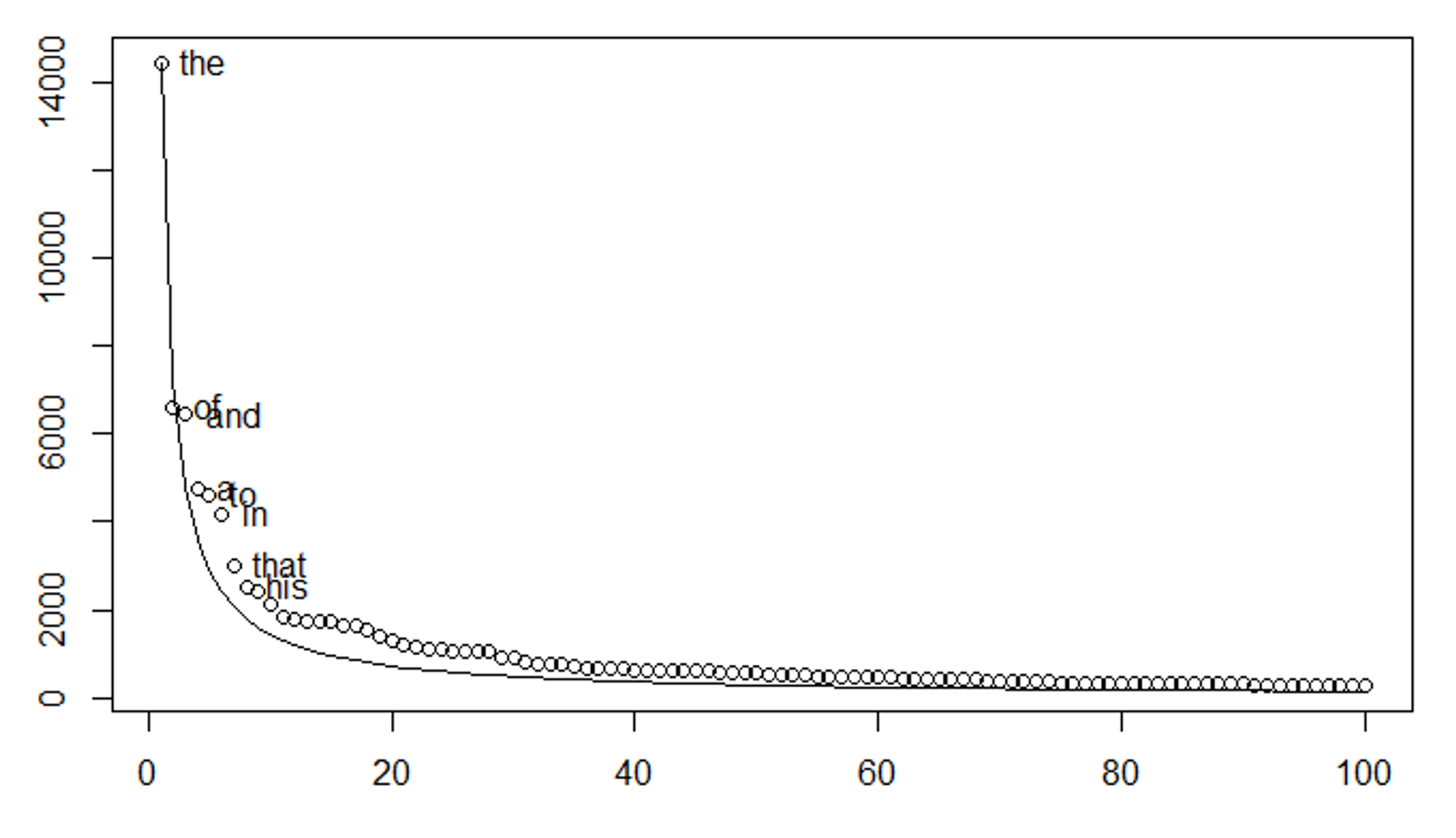
The word "the" shows up about twice as often as "of," which shows up about twice as often as "and." Keep going down the list and this pattern still holds. The 100th most common word appears roughly 100 times less often than the most common. The 1,000th appears 1,000 times less. The 10,000th, about 10,000 times less.

This isn't a coincidence or some quirk of English—it's called Zipf's Law, and it shows up in every human language ever studied. If you are looking for an awesome intuitive exploration, check out this old Vsauce video.

But what you need to know is that all natural language follows this distribution with freaky consistency: the frequency of any word is inversely proportional to its rank, following f(r) ∝ 1/r^α where α ≈ 1. This spans 4-6 orders of magnitude, from words you see multiple times per sentence to technical terms appearing once in an entire corpus.

This is also why chatbots can't find technical documentation, why search returns generic results instead of specialized matches, why RAG systems fail —and why AI writing sounds the way it does.

Why We Turn Words Into Numbers

Computers don't understand words—they process numbers. But the problem runs deeper than just thinking about data types.

Consider the word "bank": one string, two completely different concepts (financial institution vs. river edge). Same spelling, same pronunciation, entirely different semantics. Scale this ambiguity across millions of words, each with multiple meanings, contextual variations, and complex relationships to other words, and you see why explicit rule-based approaches are mathematically intractable.

Every AI system that works with language (think search engines, chatbots, recommendation systems, document analysis tools) needs some way to convert text into mathematics that captures semantic meaning, not just character sequences.

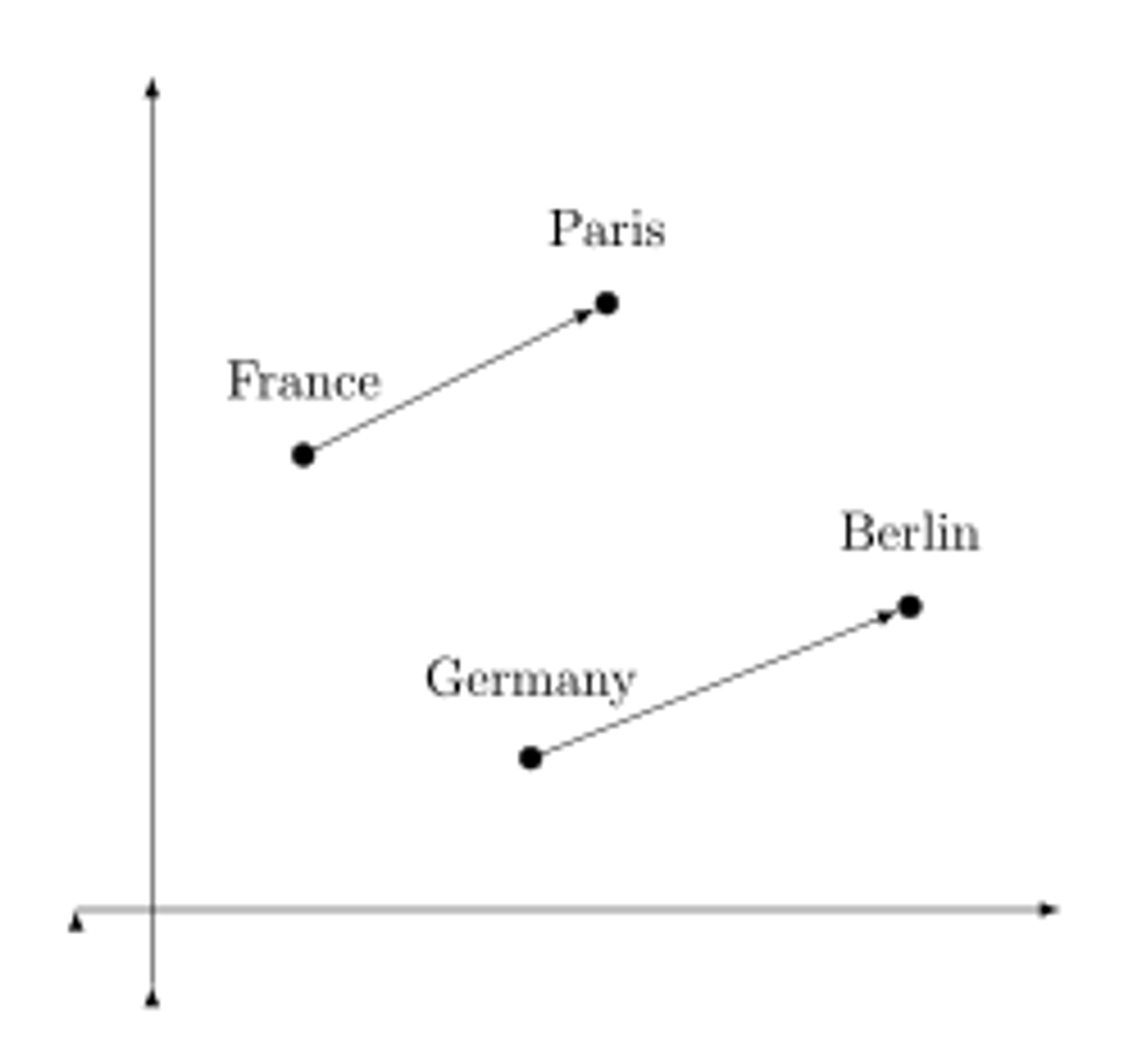
You can't do any of this with raw text. You need mathematical representations that capture semantic relationships—that "king" relates to "queen" in similar ways that "man" relates to "woman." That "Paris" and "France" have a geographic relationship similar to "Berlin" and "Germany." That "running" and "jogging" are more similar than "running" and "sleeping."

The solution we've developed is called embeddings: neural networks that map each word to a point in high-dimensional space, typically 768 or 1024 dimensions. Words with similar meanings get positioned nearby. "Doctor" sits close to "physician." "Happy" near "joyful." Every semantic relationship becomes geometric—distances, angles, and neighborhoods in this numerical space.

This approach powers virtually every modern AI system, and there's really no other alternative at scale. You cannot write explicit rules for how every word relates to every other word across millions of vocabulary items. Human language is too complex, too ambiguous, too creative. The only tractable approach is learning these relationships from data by representing language mathematically.

Which brings us to the fundamental problem: we're trying to represent a power-law distribution using fixed-capacity containers!

Power Laws Meet Euclidean Space

We're attempting to represent Zipf's exponential distribution using fixed-size vectors—uniform-capacity containers. Every word gets the same dimensional budget, whether it's "the" (appearing billions of times in training data) or "thrombocytopenia" (appearing maybe a few dozen times). We're compressing a power-law distribution into uniform-capacity containers.

The dimension problem runs deeper than just running out of space. It's a fundamental mismatch between the structure of language and the geometry of our numerical representations. Embedding models attempt to represent Zipfian distributions into fixed-dimensional Euclidean space.

The Johnson-Lindenstrauss lemma provides the mathematical lower bound: preserving distances between n points with ε-distortion requires k ≥ 4log(n)/(ε² - ε³/3) dimensions. For a 50,000 word vocabulary with 10% distortion tolerance, this demands approximately 5,300 dimensions—yet standard BERT uses only 768.

And still this mismatch runs deeper.

Hyperbolic space provides exponential volume growth (V(r) ∝ sinh^(d-1)(r)), naturally matching hierarchical power-law structures, while Euclidean space offers only polynomial growth (V(r) ∝ r^d).

Research by Nickel and Kiela demonstrated that representing tree-like structures requires O(n) dimensions in Euclidean space but only O(log n) in hyperbolic space. Language, with its Zipfian distribution and hierarchical semantic relationships, inherently exhibits the structure that Euclidean embeddings handle poorly.

To bring this up a little bit, imagine trying to store an exponentially growing library in a fixed-size warehouse. The popular books all fit (they''re common enough that even with limited space, you can represent them well), but as soon as you move to rarer books, you're forced to stack them in corners, compress their information, or simply fail to capture their unique characteristics.

The warehouse's fixed capacity creates an information bottleneck that disproportionately affects the rare items. When you turn language into numbers using standard methods, you're forcing an exponentially structured distribution into a linearly structured space.

Something has to give, and what gives is representation quality for rare words.

Why Does AI Writing Sound Like That?

Let's put this into the context of something that everyone reading this can relate to.

There's just something about AI-generated text that makes it recognizable, even when it's technically correct and coherent. It isn't necessarily a stylistic choice or even a quirk of training data curation, it's actually the same math we've been discussing, made visible in prose.

AI writing defaults to the head of the Zipfian distribution because that's where the model's representational capacity concentrates.

Consider these patterns:

Common phrasing over precise terminology: An AI writing about machine learning will readily use "neural network" (high frequency, well-represented) but struggle with "heteroscedastic uncertainty" (rare, poorly represented). It might say "important factor" instead of "confounding variable," "makes worse" instead of "exacerbates," "related to" instead of "orthogonal to."

Not because it doesn't "know" the precise terms, but because the embedding space for those rare terms is geometrically poorly conditioned (which generally manifests as high perplexity, uncertain neighborhoods, and weak gradient convergence during training).

Generic descriptors over distinctive detail: So why does AI prose tend toward phrases like "delve into," "tapestry of," "it's important to note," and "multifaceted"? Well, these phrases occupy a sweet spot in the frequency distribution. They are common enough to be well-represented, and vague enough to fit many contexts.

The mathematical pressure is always toward maximum likelihood, and the most likely words are, by definition, the most common ones. The gradient descent that trained the model saw "delve into" thousands of times more often than "excavate," "probe," or "dissect." Now, almost every Medium article "delves" into their topic.

Resistance to technical jargon: When generating text about specialized domains, AI models exhibit a measurable tendency to paraphrase technical terms into common language. A model writing about database systems might replace "ACID transactions" with "reliable database operations," or "denormalization" with "combining tables for faster queries." This is the model gravitating toward vocabulary where its representations are mathematically robust. Again, we see that the rare technical terms live in poorly-trained regions of the embedding space.

The underlying mechanism for all of these patterns is cross-entropy loss:

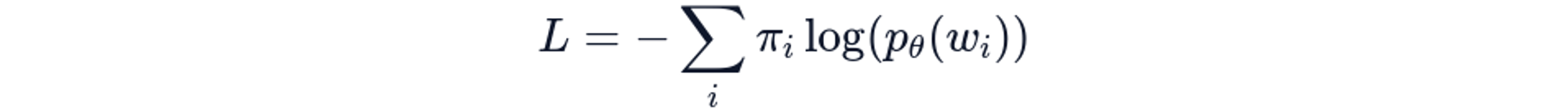
Which makes the model optimizes for likely words, not precise words.

The probability mass concentrates where training signal concentrated. Generation is the inverse of embedding—and both suffer from the same Zipfian distribution mismatch!

This is why fine-tuning on domain-specific data can actually change writing style, not just augment retrieval!

When you fine-tune a model on legal documents, medical literature, or technical documentation, you're rebalancing the gradient distribution as a whole. Facts and any corresponding style. Think about the tone of a corpus of academic papers vs. fashion magazines- the way that sentences and jargon are structured are completely different.

When a model is trained on a huge amount of human data, all of these different ways of speaking and composing language boil down to a least common denominator parlance - the parlance that you see whenever you chat with a language model.

When you fine-tune, you''re giving rare domain-specific terms more training signal, better embedding geometry, and lower perplexity. The model's writing becomes more domain-appropriate not through memorization but through this mathematical reweighting of the vocabulary distribution.

The "AI voice" is Zipf's Law made audible. It's what happens when a power-law distribution gets forced through frequency-proportional training into fixed-capacity representations. The same mathematical constraints that prevent embeddings from representing rare words well also prevent language models from generating them naturally.

How this Results in Production Failures

All of these theoretical limitations we have been discussing manifest as concrete failures in enterprise deployments. According to S&P Global Market Intelligence, 42% of companies abandoned most AI initiatives in 2025—up from just 17% in 2024. Analysis identifies 'missed retrieval' and 'wrong format' as common failure modes directly related to long-tail vocabulary handling.

Anthropic's contextual retrieval research documented specific cases: "Error code TS-999" queries fail with semantic embeddings alone because models find content about "error codes in general" but miss exact matches. The solution required hybrid approaches combining BM25 lexical matching with semantic embeddings—acknowledging that single-vector semantic models inherently struggle with exact rare term matching.

Code search presents amplified challenges. In technical documentation, "snowflake" should be closest to "databricks" and "redshift" (data warehousing platforms), not "rain" or "winter"—but general embeddings lack domain context for this distinction. The vocabulary consists heavily of rare technical terms, product names, API functions, and error codes, all occupying the long tail where general models fail.

The business case becomes clear: custom infrastructure investment shows strong ROI in specialized domains. Voyage AI's legal model delivers 10%+ accuracy improvements on complex legal retrieval. Harvey AI's partnership with PwC achieved 91% preference over ChatGPT for tax assistance—a domain where specialized tax code terminology dominates queries.

Building Better Number Systems

The decision framework balances accuracy requirements against infrastructure investment. Fine-tuning provides middle ground: LlamaIndex demonstrated 5-10% performance increases with fine-tuned BGE models using just 1,000-6,000 training pairs. Sentence Transformers 3 made fine-tuning accessible with training completing in 3 minutes on consumer GPUs using synthetic LLM-generated datasets.

The rule of thumb is to build custom when the accuracy gap exceeds 10% and volume justifies investment. Legal, medical, and financial domains show the clearest cases: vocabulary overlap with general models below 60%, mission-critical applications where errors are costly, and high-volume usage spreading infrastructure costs across many queries.

Technical Approaches

The technical approach layers multiple strategies to address different aspects of the Zipfian distribution challenge:

Hybrid retrieval is one method, and we cover it in pretty deep detail here.

Domain-specific tokenization proves to be another very effective tool. Medical embedding research found that extending tokenizer vocabulary to 52,543 tokens incorporating PubMed terminology reduced tokenization inefficiency substantially. Standard BPE tokenization fragments rare technical terms into subword units, losing semantic coherence. Domain-specific vocabularies preserve these terms as single tokens, allowing dedicated embedding capacity.

Frequency-aware training helps too as it addresses gradient dynamics directly. Applying token-dependent learning rates α_token ∝ 1/√frequency provably improves convergence on imbalanced data. The learning rate modification compensates for the π_i frequency imbalance in gradient appearance, providing rare tokens with proportionally larger updates when they do appear.

Another trick is gradient gating (AGG). It can reduce rare token perplexity from 813.76 to 75.39 (90.7% improvement!!) by modifying gradient flow during backpropagation. The technique applies selective amplification:

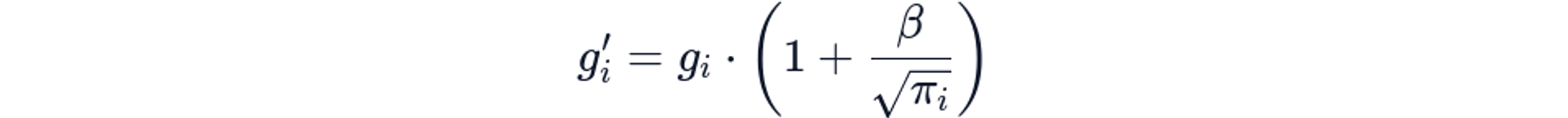
Where β controls amplification strength and π_i is token frequency. This effectively rebalances the cross-entropy loss to weight rare tokens more heavily during optimization.

And as always, architecture selection depends on specific constraints! Again check out this article where we dive a little deeper on the architecture of embeddings models and how we at Sylow are building these systems :)

• Single-vector dense embeddings (BERT, sentence-transformers): Suit low-latency requirements under 10ms and memory-constrained deployments. Trade representation quality for efficiency. Typical storage: 768-1024 floats per item.
• Multi-vector ColBERT: Excels for complex queries and out-of-domain retrieval by maintaining separate vectors for each token, accepting 20-100x storage overhead. Enables late interaction: relevance computed as Σ_i max_j E_q[i] · E_d[j] where each token maintains geometric fidelity. Better handles long-tail terms by avoiding compression into single vector.
• Sparse SPLADE: Handles rare terminology and exact keyword matching through learned sparse representations. Expands vocabulary to 30K-50K dimensions with <5% non-zero values. Explicitly models term importance weights that can preserve rare terms: w_t = Σ_i log(1 + ReLU(W·h_i))_t.
• Matryoshka representations: These provide deployment flexibility across multiple dimension budgets through nested optimization. Model trained such that truncating to d/2, d/4, d/8 dimensions maintains utility, enabling adaptive precision based on term frequency or resource constraints.

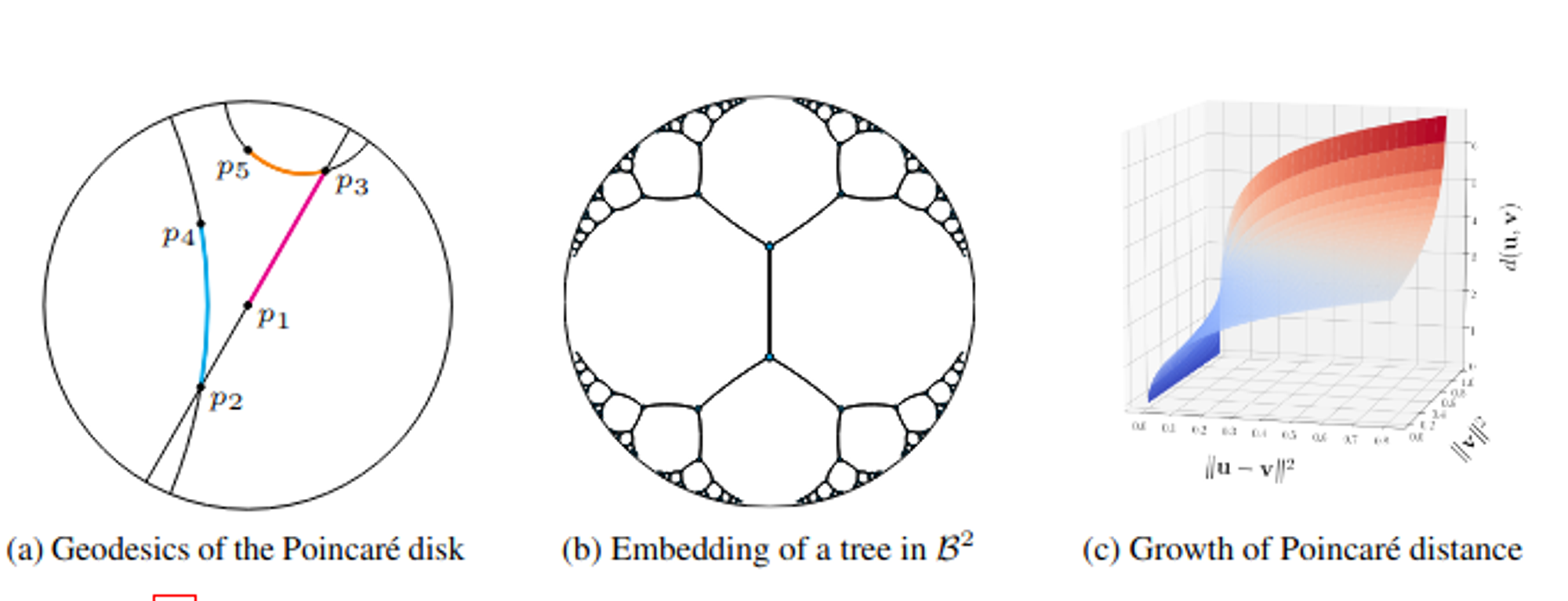
Hyperbolic embeddings directly address the geometric mismatch. Poincaré embeddings and Lorentz models provide O(log n) representation capacity for hierarchical structures versus O(n) in Euclidean space. The exponential volume growth naturally accommodates power-law distributions. Distance in hyperbolic space: d_H(x,y) = arcosh(1 + 2||x-y||²/((1-||x||²)(1-||y||²))) provides hierarchical structure matching linguistic relationships.

The Numbers We Choose Matter

The challenge of turning language into numbers isn't just an engineering problem to be solved with better algorithms or by throwing more compute at it. It's a fundamental tension between the power-law distribution of natural language and the fixed-capacity representations we use to encode it.

Zipf's law describes how language actually works: exponentially skewed, with a small number of words dominating and a long tail of rare terms carrying specialized meaning. Standard embedding approaches—uniform dimensional budgets, frequency-proportional training, Euclidean geometry—systematically fail this distribution, creating 10-100x worse representations for rare words than common ones.

The second code gets launched in production, this transforms from an academic observation to a business problem. Legal terminology, financial metrics, medical vocabulary, technical documentation, product catalogs—the specialized language defining domain expertise occupies the frequency range where general models systematically underperform.

You see this math in action every time you use AI systems: in retrieval failures that miss technical documentation, in search results that return generic matches instead of specialized terminology, in generated text that defaults to common phrasing over precise domain language.

Domain-specific infrastructure, whether through fine-tuning, custom tokenization, frequency-aware training, hyperbolic embeddings, or architectural changes, optimizes for your particular distribution's long tail.

The numbers we choose for representing language determine which language we can actually represent. Choose them to match how your language actually distributes, not how we wish it did.